羅傑·潘洛斯爵士，OM，FRS（英語：Sir Roger Penrose，1931年8月8日－），英國數學物理學家與牛津大學數學系W. W. Rouse Ball名譽教授。他在數學物理方面的工作擁有高度評價，特別是對廣義相對論與宇宙學方面的貢獻。他也是娛樂數學家與具爭議性的哲學家。羅傑·潘洛斯是科學家理昂內·潘洛斯與瑪格麗特·雷瑟斯的兒子，為數學家奧利佛·潘洛斯與西洋棋大師強納森·潘洛斯的兄弟。
他於2020年獲得諾貝爾物理學獎，因為他發現黑洞的形成有力預測了廣義相對論。
羅傑·潘洛斯以其於1974年發現潘洛斯鋪磚法著稱，能以兩種磚片非週期性地鋪滿整個平面。於1984年，類似特徵被發現在類晶體中的原子排列。他最重要的貢獻可能是他在1971年發明了自旋網路，爾後在迴圈量子重力理論中成為構成時空幾何的基礎。他在推廣通稱為潘洛斯圖的因果圖頗具影響力。
潘若斯用這兩種胖「菱形」與瘦「鳶形」的磁磚拼湊出五角對稱，
伯斯的西澳大利亞大學的分子化學大樓，
佛格森用簡單的兩種形狀，舖絮出了奇異而複雜的網狀線條，
盯著這種繁複的圖案一段時間之後，一般都會產生錯覺，
早期拼磚藝術家們多半會利用這種錯覺，以顏色、
同樣地，西澳大利亞大學的拼磚也沒有任何呈現立體感的深淺著色，
MOSAIC SOPHISTICATION A quasi-crystalline Penrose pattern at the Darb-i Imam shrine in Isfahan, Iran.
In the beauty and geometric complexity of tile mosaics on walls of medieval Islamic buildings, scientists have recognized patterns suggesting that the designers had made a conceptual breakthrough in mathematics beginning as early as the 13th century.
A piece from a mausoleum in Turkey.
A pattern taken from a Turkish mosque.
A new study shows that the Islamic pattern-making process, far more intricate than the laying of one's bathroom floor, appears to have involved an advanced math of quasi crystals, which was not understood by modern scientists until three decades ago.
The findings, reported in the current issue of the journal Science, are a reminder of the sophistication of art, architecture and science long ago in the Islamic culture. They also challenge the assumption that the designers somehow created these elaborate patterns with only a ruler and a compass. Instead, experts say, they may have had other tools and concepts.
Two years ago, Peter J. Lu, a doctoral student in physics at Harvard University, was transfixed by the geometric pattern on a wall in Uzbekistan. It reminded him of what mathematicians call quasi-crystalline designs. These were demonstrated in the early 1970s by Roger Penrose, a mathematician and cosmologist at the University of Oxford.
Mr. Lu set about examining pictures of other tile mosaics from Afghanistan, Iran, Iraq and Turkey, working with Paul J. Steinhardt, a Princeton cosmologist who is an authority on quasi crystals and had been Mr. Lu's undergraduate adviser. The research was a bit like trying to figure out the design principle of a jigsaw puzzle, Mr. Lu said in an interview.
In their journal report, Mr. Lu and Dr. Steinhardt concluded that by the 15th century, Islamic designers and artisans had developed techniques "to construct nearly perfect quasi-crystalline Penrose patterns, five centuries before discovery in the West."
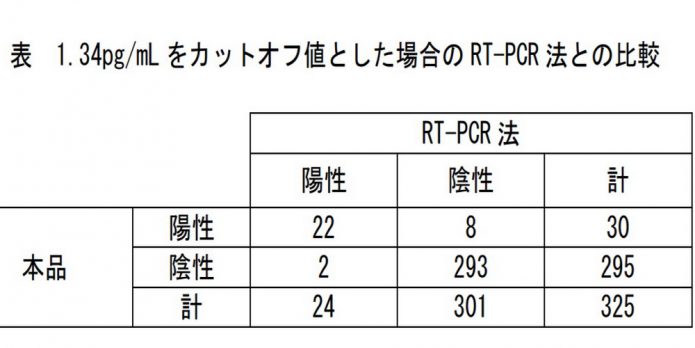
Some of the most complex patterns, called "girih" in Persian, consist of sets of contiguous polygons fitted together with little distortion and no gaps. Running through each polygon (a decagon, pentagon, diamond, bowtie or hexagon) is a decorative line. Mr. Lu found that the interlocking tiles were arranged in predictable ways to create a pattern that never repeats — that is, quasi crystals.
"Again and again, girih tiles provide logical explanations for complicated designs," Mr. Lu said in a news release from Harvard.
He and Dr. Steinhardt recognized that the artisans in the 13th century had begun creating mosaic patterns in this way. The geometric star-and-polygon girihs, as quasi crystals, can be rotated a certain number of degrees, say one-fifth of a circle, to positions from which other tiles are fitted. As such, this makes possible a pattern that is infinitely big and yet the pattern never repeats itself, unlike the tiles on the typical floor.
This was, the scientists wrote, "an important breakthrough in Islamic mathematics and design."
Dr. Steinhardt said in an interview that it was not clear how well the Islamic designers understood all the elements they were applying to the construction of these patterns. "I can just say what's on the walls," he said.
Mr. Lu said that it would be "incredible if it were all coincidence."
"At the very least," he said, "it shows us a culture that we often don't credit enough was far more advanced than we ever thought before."
From a study of a few hundred examples, Mr. Lu and Dr. Steinhardt determined that the technique was fully developed two centuries later in mosques, palaces, shrines and other buildings. They noted that "a nearly perfect quasi-crystalline Penrose pattern" is found on the Darb-i Imam shrine in Isfahan, Iran, which was built in 1453. The researchers described how the architects there had created overlapping patterns with girih tiles at two sizes to produce nearly perfect quasi-crystalline patterns.
In the report, Mr. Lu and Dr. Steinhardt said the examples they had studied so far "fall just short of being perfect quasi crystals; there may be more interesting examples yet to be discovered."
In a separate article in Science, some experts in the math of crystals questioned if the findings were an entirely new insight. In particular, Emil Makovicky of the University of Copenhagen in Denmark said the new report failed to give sufficient credit to an analysis he published in 1992 of mosaic patterns on a tomb in Iran.
Mr. Lu and Dr. Steinhardt said they regretted what they called a misunderstanding. They pointed out that the length of their report was strictly enforced by journal editors, but it did include two footnotes to Dr. Makovicky's research. None of the referees or editors who reviewed the paper, Dr. Steinhardt said, asked for more attention to the previous research.
Although their work had some elements in common with Dr. Makovicky's, Dr. Steinhardt said in an interview that their research dealt with not one but a "whole sweep of tilings" interpreted through a few hundred examples.
The article quoted two other experts, Dov Levine and Joshua Socolar, physicists at the Israel Institute of Technology in Haifa and Duke University, respectively, as agreeing that Dr. Makovicky deserved more credit. But, the article noted, they said the Lu-Steinhardt research had "generated interesting and testable hypotheses."
hc:
實際上，此番沒多少新意。他說Superpower 一書出版二年來的中美產業重點之分，是虛的，也非重點。樂觀的只是應用，而這方面，各國政府/人民願接受的風險/不完美，而非技術的突破，例如自動駕駛，美國可能領先，但其政府/人民的安全要求相對中國高.....。
2020年諾貝爾生理學或醫學獎
共同
Harvey J. Alter，Michael Houghton和Charles M. Rice
用於發現丙型肝炎病毒
今年的諾貝爾獎授予了三位科學家，他們在與血源性肝炎的鬥爭中做出了決定性的貢獻。血源性肝炎是導致世界各地人們肝硬化和肝癌的主要全球性健康問題。
Harvey J. Alter，Michael Houghton和Charles M. Rice做出了開創性發現，從而鑑定出一種新型病毒，即丙型肝炎病毒。在開展工作之前，發現甲型和乙型肝炎病毒是向前邁出的關鍵步驟，但大多數血源性肝炎病例仍無法解釋。丙型肝炎病毒的發現揭示了剩餘的慢性肝炎病例的病因，並使血液檢測和新藥成為可能，挽救了數百萬人的生命。
肝炎或肝炎，是希臘語中“肝和炎症”的組合詞，主要是由病毒感染引起的，儘管酗酒，環境毒素和自身免疫性疾病也是重要的原因。在1940年代，很明顯有兩種主要類型的傳染性肝炎。第一種稱為甲型肝炎，是通過污水或食物傳播的，通常對患者幾乎沒有長期影響。第二種是通過血液和體液傳播的，它代表著更為嚴重的威脅，因為它會導致慢性疾病，並發展為肝硬化和肝癌（圖1）。）。這種形式的肝炎是隱性的，因為否則健康個體可以在嚴重並發症出現之前靜默感染多年。血源性肝炎與高發病率和高死亡率相關，每年在世界範圍內造成超過一百萬的死亡，因此使其成為與HIV感染和結核病相當的全球性健康問題。
圖1肝炎有兩種主要形式。一種形式是由甲型肝炎病毒引起的急性疾病，這種病毒是由受污染的水或食物傳播的。另一種形式是由乙型肝炎病毒或丙型肝炎病毒引起的（今年的諾貝爾獎）。這種形式的血源性肝炎通常是一種慢性疾病，可能會發展為肝硬化和肝細胞癌。
成功干預傳染病的關鍵是確定病原體。在1960年代，Baruch Blumberg確定一種形式的血源性肝炎是由一種被稱為乙型肝炎病毒的病毒引起的，這一發現導致了診斷測試和有效疫苗的發展。由於這一發現，布倫伯格被授予1976年諾貝爾生理學或醫學獎。
當時，美國國立衛生研究院的Harvey J. Alter研究了接受輸血的患者中肝炎的發生情況。儘管對新發現的乙型肝炎病毒進行的血液檢查減少了與輸血有關的肝炎的病例數，但Alter及其同事令人擔憂地證明仍有大量病例存在。大約在這段時間也進行了甲型肝炎病毒感染的檢測，很明顯，甲型肝炎不是這些原因不明的原因。
令人擔憂的是，大量輸血者由於未知的傳染原而患上了慢性肝炎。Alter和他的同事表明，這些肝炎患者的血液可以將疾病傳播給黑猩猩，這是人類之外唯一的易感宿主。隨後的研究還表明，未知的傳染原具有病毒的特徵。Alter的方法研究以這種方式定義了一種新型的，獨特形式的慢性病毒性肝炎。這種神秘的疾病被稱為“非甲，非乙”肝炎。
現在，鑑定新型病毒是當務之急。儘管使用了所有傳統的病毒搜尋技術，但儘管如此，病毒仍無法隔離已有十多年的歷史。在Chiron製藥公司工作的Michael Houghton進行了分離病毒遺傳序列所需的艱鉅工作。霍頓和他的同事們從感染黑猩猩血液中發現的核酸中提取了DNA片段。這些片段大部分來自黑猩猩本身的基因組，但研究人員預測，其中一些片段將來自未知病毒。假設從肝炎患者的血液中會存在針對病毒的抗體，研究人員使用患者血清來鑑定克隆的編碼病毒蛋白的病毒DNA片段。經過全面搜索，發現了一個陽性克隆。進一步的工作表明，該克隆源自一種新型的RNA病毒，屬於黃病毒家族，它被命名為丙型肝炎病毒。慢性肝炎患者中抗體的存在強烈暗示了這種病毒是缺少的因素。
圖2本年度諾貝爾獎授予的發現摘要。Harvey J. Alter進行的輸血相關性肝炎的方法研究表明，未知病毒是導致慢性肝炎的常見原因。邁克爾·霍頓（Michael Houghton）使用未經測試的策略來分離名為丙型肝炎病毒的新病毒的基因組。查爾斯·賴斯（Charles M. Rice）提供了最後證據，證明僅丙型肝炎病毒即可引起肝炎。
丙型肝炎病毒的發現具有決定性意義。但是，這個難題的一個基本要素卻沒有得到解決：僅病毒本身就能引起肝炎嗎？為了回答這個問題，科學家不得不研究克隆的病毒是否能夠複製並引起疾病。聖路易斯華盛頓大學的研究員查爾斯·賴斯（Charles M. Rice）以及其他研究RNA病毒的小組指出，丙型肝炎病毒基因組末端的一個先前未知的區域，他們懷疑這可能對病毒複製很重要。賴斯還觀察到分離出的病毒樣本中的遺傳變異，並假設其中一些可能會阻礙病毒複製。通過基因工程，賴斯產生了丙型肝炎病毒的RNA變異體，其中包括病毒基因組的新定義區域，並且沒有失活的遺傳變異。將這種RNA注射到黑猩猩的肝臟中後，在血液中檢測到病毒，並觀察到與慢性病患者相似的病理變化。這是僅丙型肝炎病毒可能導致無法解釋的輸血介導的肝炎病例的最終證據。
諾貝爾獎獲得者發現丙型肝炎病毒是正在進行的與病毒性疾病鬥爭的里程碑式成就（圖2）。由於他們的發現，現在可以對該病毒進行高度敏感的血液檢查，並且這些檢查基本上已經消除了世界許多地方的輸血後肝炎，從而大大改善了全球健康狀況。他們的發現還使針對丙型肝炎的抗病毒藥物得以快速發展。歷史上首次可以治愈該病，這為從世界人口中根除丙型肝炎病毒帶來了希望。為了實現這一目標，將需要國際努力以促進血液測試和在全球範圍內提供抗病毒藥物（圖3）。
圖3三位諾貝爾獎獲得者的發現允許設計敏感的血液測試，從而消除了世界上大部分地區通過輸血傳播的肝炎的風險。這一突破也使開發可以治愈該疾病的抗病毒藥物成為可能。丙型肝炎仍然是全球主要的健康問題，但是現在存在消除這種疾病的機會。
Alter HJ，Holland PV，Purcell RH，Lander JJ，Feinstone SM，Morrow AG，Schmidt PJ。排除商業和乙型肝炎抗原陽性供體後的輸血後肝炎。安實習生。1972年；77：691-699。
Feinstone SM，Kapikian AZ，Purcell RH，Alter HJ和Holland PV。與輸血相關的肝炎不是由於A型或B型病毒性肝炎引起的。N Engl J Med。1975年；292：767-770。
Alter HJ，Holland PV，Morrow AG，Purcell RH，Feinstone SM，Moritsugu Y.與輸血相關的肝炎的臨床和血清學分析。柳葉刀。1975年；2：838-841。
Alter HJ，Purcell RH，Holland PV，PopperH。非甲非乙型肝炎的可傳播藥物。柳葉刀。1978年；1：459-463。
Choo QL，Kou G，Weiner AJ，Overby LR，Bradley DW，HoughtonM。分離源自血源性非A，非B病毒性肝炎基因組的cDNA克隆。科學。1989年；244：359-362。
Kuo G.，Choo QL，Alter HJ，Gitnick GL，Redeker AG，Purcell RH，Miyamura T，Dienstag JL，Alter CE，Stevens CE，Tegtmeier GE，Bonino F，Colombo M，Lee WS，Kuo C.，Berger K， Shuster JR，Overby LR，Bradley DW，HoughtonM。一種針對人非甲非乙型肝炎主要病原性病毒的循環抗體的測定方法。科學。1989年；244：362-364。
Kolykhalov AA，Agapov EV，Blight KJ，Mihalik K，Feinstone SM，Rice CM。通過肝內接種轉錄的RNA傳播丙型肝炎。科學。1997; 277：570-574。
Harvey J. Alter於1935年出生於紐約。他在羅切斯特大學醫學院獲得醫學學位，並在斯特朗紀念醫院和西雅圖大學醫院接受內科醫學培訓。1961年，他加入國立衛生研究院（NIH），擔任臨床助理。他在喬治敦大學（Georgetown University）工作了幾年，然後於1969年返回NIH，加入了臨床中心輸血醫學系，擔任高級研究員。
邁克爾·霍頓（Michael Houghton）出生於英國。他於1977年從倫敦國王學院獲得博士學位。他於1982年加入GD Searle＆Company，之後於1982年移居加利福尼亞州埃默里維爾的Chiron公司。他於2010年移居艾伯塔大學，目前是加拿大傑出病毒學研究主席和李嘉誠病毒學教授，在艾伯塔大學任教。他還是李嘉誠應用病毒學研究所所長。
查爾斯·賴斯（Charles M. Rice）於1952年出生在薩克拉曼多。他於1981年在加州理工學院獲得博士學位，並於1981年至1985年期間接受了博士後培訓。他於1986年在聖路易斯華盛頓大學醫學院成立了研究小組，並於1995年成為正式教授。自2001年以來，他一直擔任紐約洛克菲勒大學的教授。在2001年至2018年期間，他一直是洛克菲勒大學丙型肝炎研究中心的科學與執行主任，並一直活躍在該中心。
插圖：©諾貝爾生理學或醫學委員會。插圖畫家：MattiasKarlén
