恐引發基督教世界激烈辯論
〔編 譯俞智敏/綜合報導〕專研基督教歷史的哈佛大學神學院教授金恩(Karen King),18日公布一份公元4世紀的莎草紙,上面用古埃及科普特文字引述耶穌明確提到他的「妻子」。這項發現恐在基督教世界再度引發耶穌是否結婚的激 烈辯論,甚至可能推翻基督教崇尚禁欲的理想。
金恩教授是在羅馬舉行的一場國際科普特研究會議中,公布這張長7.6公分、寬3.8公分,面積 小於一張名片的莎草紙碎片。金恩表示,這張碎片是用科普特文抄寫的福音書,可能是由希臘人在公元2世紀寫成,然後再被轉譯為科普特文。紙片上的4個科普特 文字可翻譯為「耶穌對他們說,我的妻子」,首度證明部分早期基督徒相信耶穌曾經結婚。研究人員認為,耶穌這裡指的就是抹大拉的馬利亞。
早期基督徒相信耶穌曾結婚
金恩把這張莎草紙片稱為「耶穌之妻福音」,她表示這並不能證明耶穌確曾結婚,卻論及當時基督徒所面臨的家庭和婚姻等議題。金恩還說,在上述對話中,耶穌門徒們討論馬利亞是否值得尊敬,而耶穌回答說,「她可以當我的門徒」。
儘管缺乏可靠的歷史證據支持,基督教傳統上一直認為耶穌未婚,但有關耶穌曾結婚的說法不時浮上檯面。
暢銷書作家丹布朗也在「達文西密碼」一書中,將耶穌和抹大拉的馬利亞描寫為夫妻。
金恩認為,這份新福音顯示耶穌是否結婚的問題,源於基督徒對性與婚姻的激烈討論,直到耶穌去世逾一世紀後的公元200年左右,神學家亞力山卓的克里門才開始提出耶穌未曾結婚的說法。
這張莎草紙屬於一位匿名收藏家所有,這位收藏家請金恩協助翻譯並分析文字內容,紙片的發現狀況不明,但金恩認為紙片是來自埃及,當地的乾燥氣候使得古文獻得以保存至今,紙片上的文字也是古代埃及所使用的文字。
學者︰文件來源不明應謹慎
但 另一位聖經學者、肯塔基州亞斯里神學院教授威特林頓表示,由於文件來源不明,分析時應更為謹慎。威特林頓認為,這份文件類似西元2、3及4世紀的諾斯替 (Gnostic )文件模式,使用親密語言來討論靈性關係。諾斯替教派常提到一種被稱為「姊妹—妻子」的文件,他們會帶著一位女性信徒隨行,負責煮食、打掃或其他家務,但 彼此間並不存在性關係。
日數學家 可望證明abc猜想
「abc 猜想」是由歐洲數學家馬瑟(David Masser )與奧斯達利(Joseph Oesterle)在1985年分別提出,以a和b兩個整數及其相加後新的整數c,abc三個數組與各個質數之間的關係,可說是一個針對質數之間深層聯繫 的猜想。近30年來,許多數學家都想證明這個猜想,荷蘭萊頓大學數學研究所甚至成立一個網站計算平台「ABC@Home」,協助數學家破解這個猜想。
500頁論文 花10年才完成
望 月這篇長達4章、共500頁的論文,花了10年時間才完成,8月起在英國科學期刊「自然」網路版上公開,立即在數學界引發話題。美國哥倫比亞大學數學家戈 德菲德(Dorian Goldfeld)說,如果abc猜想獲得證實,將一舉解決眾多著名的「不定方程」(Diophantine,又稱「丟番圖」)問題,其中也包括花了 350多年才破解的費馬最後定理(Fermat Last Theorem)。
和許多丟番圖問題一樣,abc猜想是一個質數(指在一個大於 1的自然數中,除1和此整數自身外,無法被其他自然數整除的數,也可定義為只有1和本身兩個因數的數)之間關係的問題。美國史丹福大學數學系教授康拉德 (Brian Conrad)認為,在a、b和a+b的質數因數之間存在更深層的關聯。許多數學家投注大量心力試圖證明這一猜想。2007年,在法國數學家施皮羅 (Lucien Szpiro)1978年研究工作的基礎上,首次宣佈對abc猜想的證明,但很快就發現其中存在缺陷。
現年43歲的望月本身也是個傳奇人物,他雖在東京出生,但5歲時隨著父親定居美國,具有數學天分的他,16歲便跳級進入美國普林斯頓大學,19歲從數學系畢業,23歲回到日本在京大擔任助教,32歲就升任京大教授。
From Wikipedia, the free encyclopedia
In mathematics, a Diophantine equation is an indeterminate polynomial equation that allows the variables to be integers
only. Diophantine problems have fewer equations than unknown variables
and involve finding integers that work correctly for all equations. In
more technical language, they define an algebraic curve, algebraic surface, or more general object, and ask about the lattice points on it.The word Diophantine refers to the Hellenistic mathematician of the 3rd century, Diophantus of Alexandria, who made a study of such equations and was one of the first mathematicians to introduce symbolism into algebra. The mathematical study of Diophantine problems Diophantus initiated is now called "Diophantine analysis". A linear Diophantine equation is an equation between two sums of monomials of degree zero or one.
While individual equations present a kind of puzzle and have been considered throughout history, the formulation of general theories of Diophantine equations (beyond the theory of quadratic forms) was an achievement of the twentieth century.
Contents |
Examples of Diophantine equations
| In the following Diophantine equations, x, y, and z are the unknowns, the other letters being given are constants. | |
 |
This is a linear Diophantine equation (see the section "Linear Diophantine equations" below). |
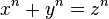 |
For n = 2 there are infinitely many solutions (x,y,z): the Pythagorean triples. For larger values of n, Fermat's Last Theorem states there are no positive integer solutions (x, y, z). |
 |
(Pell's equation) which is named after the English mathematician John Pell. It was studied by Brahmagupta in the 7th century, as well as by Fermat in the 17th century. |
 |
The Erdős–Straus conjecture states that, for every positive integer n ≥ 2, there exists a solution in x, y, and z, all as positive integers. Although not usually stated in polynomial form, this example is equivalent to the polynomial equation 4xyz = yzn + xzn + xyn = n(yz + xz + xy). |
沒有留言:
張貼留言