Mathematics and Art: A Cultural History by Lynn Gamwell

Why the history of maths is also the history of art


In her new book Mathematics and Art, historian Lyn Gamwell explores how artists have for thousands of years used mathematical concepts - such as infinity, number and form - in their work. Here she choses ten stunning images from her book that reveal connections between maths and art.
Detail of Karl Gerstner’s Polychrome of Pure Colors. For full credit see full image below.


Lynn Gamwell

Wednesday 2 December 201506.55 GMTLast modified on Wednesday 2 December 201510.13 GMT



When I was a graduate student in art history, I read many explanations of abstract art, but they were invariably inadequate and misleading. So after completing my PhD, I went on to learn the history of biology, physics, and astronomy, and to publish a book detailing how modern art is an expression of the scientific worldview.

Yet many artworks also express the mathematics and technology of their times. To research Math and Art I had to learn maths concepts like calculus, group theory and predicate logic. As a novice struggling to understand these ideas, I was struck with the poor quality and confusing content of illustrations in most educational books. So I vowed to create for my book a set of cogent math diagrams that are crystal-clear visualizations of the abstract concepts.

As a lecturer at the School of Visual Arts in Manhattan, I wrote this book for my students, such as Maria, who told me she was never good at history because she couldn’t remember dates, and for Jin Sug, who failed high school algebra because he couldn’t memorize formulae. I hope they will read this book and discover that history is a storybook and that math is about captivating ideas.

Here are ten images followed by descriptions:
FacebookTwitterPinterest Eric J. Heller (American, born 1946), Transport VI, ca. 2000. Digital print. Courtesy of the artist.

Throughout history, scientists have discovered mathematical patterns in nature, such as the paths taken by electrons as they flow over the hills and valleys of tiny “landscapes” that are measured in microns (one micron equals one millionth of a meter). Paths of electrons in this digital print were recorded by Eric J. Heller, who studies rogue waves (freak waves, killer waves) on large and small scales. When a wave of electrons flows through a computer, a freak wave in a semiconductor can suddenly threaten the smooth functioning of the device.
FacebookTwitterPinterest Jim Sanborn (American, b. 1945), Kilkee County Clare, Ireland, 1997. Large-format projection, digital print, 30 × 36 in. (76.2 × 91.4 cm). Courtesy of the artist.

Western mathematics proceeds by increasing abstraction and generalization. In the Renaissance the Italian architect Filippo Brunelleschi invented linear perspective, a method to project geometric objects onto a “picture plane” from a given viewpoint. Three centuries later the French mathematician Jean-Victor Poncelet generalized perspective into projective geometry for planes that are tipped or rotated. Then in the early twentieth century the Dutchman L.E.J. Brouwer generalized Poncelet’s projective geometry to projections onto surfaces that are stretched or distorted into any shape—so-called rubber-sheet geometry—provided that the plane remains continuous (with no holes or tears), which is the subject of this photograph. The contemporary artist Jim Sanborn created it by projecting a pattern of concentric circles onto a large rock formation at night from about 1/2 mile away. He then took this photograph with a long exposure at moonrise.
FacebookTwitterPinterest Reza Sarhangi (Iranian-born American, b. 1952) and Robert Fathauer (American, b. 1960),Būzjānī’s Heptagon, 2007. Digital print, 13 × 13 in. (33 × 33 cm). Courtesy of the artists.

Knowledge of ancient Greek mathematics, such as Euclid and Ptolemy, was lost to the medieval West, but Islamic scholars preserved their writings in Arabic translations. In the ninth century, caliphs established the House of Wisdom in Baghdad as a place for scholars to acquire and translate foreign texts in mathematics and philosophy. Ptolemy’s thirteen-volume work is known today by the name they gave it, Almagest (Arabic for “the greatest”).

Two contemporary mathematicians, Reza Sarhangi and Robert Fathauer, pay homage to the Islamic mathematician Abū al-Wafā’ Būzjānī (AD 940¬–98), who worked at the House of Wisdom, where he wrote a practical text, On Those Parts of Geometry Needed by Craftsmen. He showed how to construct a regular heptagon (a polygon with seven equal sides and angles), which is in the center portion of this print. Around the perimeter of the heptagon Sarhangi and Fathauer wrote Buzjani’s name seven times in Farsi, the language of Persia (modern Iran).
FacebookTwitterPinterest Robert Bosch (American, b. 1963), Knot? 2006. Digital print, 34 × 34 in. (86.3 × 86.3 cm). Courtesy of the artist.

With the development of railroads in the nineteenth century, the topic of finding an optimal route for a journey was of practical interest. The topic entered the mathematics literature in 1930, when the Viennese mathematician Karl Menger described it as the “messenger problem” (das Botenproblem) of finding an optimal delivery route. It was soon dubbed the “travelling salesman’s problem”: given a list of cities and the distances between each pair, find the shortest route that visits each city once and returns to the city of origin

The American mathematician Robert Bosch drew this continuous line based on the solution to a 5000-city instance of the travelling salesman problem. From a distance, the print appears to depict a black cord against a grey background in the form of a Celtic knot. But on close inspection the apparent “grey” is actually a continuous white line moving on top of a black background. The white line never crosses over itself—it is a network rather than a knot—and so the punny answer to the title is “Not.”
FacebookTwitterPinterest Karl Gerstner (Swiss, b. 1930), Polychrome of Pure Colors, 1956-58. Printer’s ink on cubes of Plexiglas, 1 1/4 × 1 1/4 in. (3 × 3 cm). ea., fixed in a chrome-plated metal frame, 18 7/8 × 18 7/8 in. (48 × 48 cm) ea. Courtesy of the artist.

In 1905, Albert Einstein discovered the symmetry of mass and energy—mass can be converted into energy, and vice versa (E = mc2). Then in the early decades of the twentieth century, physicists and mathematicians, including Einstein, gathered in Zurich and employed group theory in their exploration of the symmetry of nature.

Swiss artists such as Gerstner created patterns that resonate with these mathematical descriptions of nature in terms of symmetry. Like the mathematicians, these artists established basic aesthetic building-blocks—units of color and form—and arranged them using rules that preserve proportion and balance.

In 1956 Gerstner devised a modular system—a movable palette with 196 hues in 28 groups—for experimenting with progressions that link form with color. Gerstner’s palette of 196 squares has 28 groups with 7 squares each. Shown here are four of myriad possible arrangements, which the artist describes using the mathematician’s terms: groups, permutations, algorithms, and invariance.
FacebookTwitterPinterest Karl Gerstner (Swiss, b. 1930), Polychrome of Pure Colors, 1956-58. Printer’s ink on cubes of Plexiglas, 1 1/4 × 1 1/4 in. (3 × 3 cm). ea., fixed in a chrome-plated metal frame, 18 7/8 × 18 7/8 in. (48 × 48 cm) ea. Courtesy of the artist.
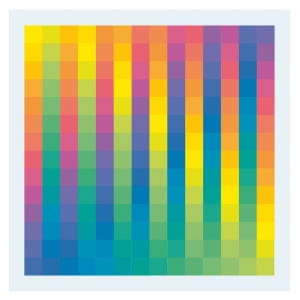
FacebookTwitterPinterest Karl Gerstner (Swiss, b. 1930), Polychrome of Pure Colors, 1956-58. Printer’s ink on cubes of Plexiglas, 1 1/4 × 1 1/4 in. (3 × 3 cm). ea., fixed in a chrome-plated metal frame, 18 7/8 × 18 7/8 in. (48 × 48 cm) ea. Courtesy of the artist.
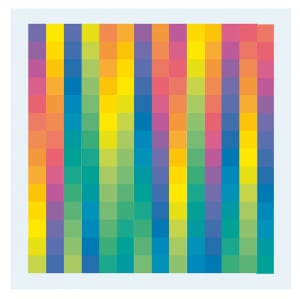
FacebookTwitterPinterest Karl Gerstner (Swiss, b. 1930), Polychrome of Pure Colors, 1956-58. Printer’s ink on cubes of Plexiglas, 1 1/4 × 1 1/4 in. (3 × 3 cm). ea., fixed in a chrome-plated metal frame, 18 7/8 × 18 7/8 in. (48 × 48 cm) ea. Courtesy of the artist.
FacebookTwitterPinterest Karl Gerstner (Swiss, b. 1930), Color Spiral Icon x65b, 2008. Acrylic on aluminum, diameter 41 in. (104 cm). Collection of Esther Grether, Basel, Switzerland.

Scientific insights into the deepest levels of the natural world are explanations based on symmetry, which the artist Karl Gerstner symbolizes with this circular “icon” for the secular age of science and technology. The most symmetrical geometric form is a sphere (all points equidistant from a point in three-dimensional space). In the late twentieth century, scientists concluded that the universe began in perfect symmetry as a point that exploded into a sphere of plasma. As the infant universe expanded, the primordial sphere cooled, and matter condensed from the plasma to form the first particles, then atoms, gas clouds, and stars. At some point the original symmetry of the universe was broken; the resulting asymmetries appear to be the result of random shifts analogous to mutations during evolution. Today physicists are recreating samples of this primordial spherical plasma to determine the degree to which the universe retains traces of its original symmetry.
FacebookTwitterPinterest Simon Thomas (British, b. 1960), Planeliner, 2005. Bead blasted stainless steel, 23 5/8 in. (60 cm) diam. × 2 1/4 in. (5.55 cm) high. Courtesy of the artist.

Simon Thomas is a young British artist whose work, such as this sculpture, is a visualization of a mathematical formula. He studied visual arts at the Royal College of Art in London in the 1980s and went on to create sculpture with striking geometric patterns, serving as artist-in-residence at the University of Bristol, both in the department of physics (1993–95) and mathematics (2002).

Mathematics and Art: A Cultural History by Lynn Gamwell is out now.

......................

This is a guest post on Alex Bellos’s maths blog. Alex’s most recent book is a mathematical colouring book, called Snowflake Seashell Star in the UK andPatterns of the Universe in the US.